
이 문제를 풀기 위해 알아야 할 내용은
곱셈공식
항등식
이렇게 2개가 있다.
곱셈공식이라는 말을 들어본 적이 있을 것이다.
사실 들어본 적이 없어도 된다.
지금부터 알면 된다.
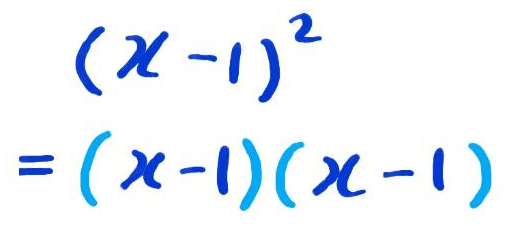
저런걸 본적 있는가?
(x-1)의 오른쪽 위에 있는 숫자는, 그 숫자만큼 (x-1)을 서로 곱하라는 말이다.
그림에 있는 숫자는 2다. 그러면 (x-1) 곱하기 (x-1)을 해주라는 말이다.
그런데 왜 중간에 곱하기 표시인 X가 없냐고?
왜 (x-1)X(x-1)이 아니고 (x-1)(x-1)이냐고?
보통 곱하기는 저렇게 생략이 가능하다.
이번 기회에 익혀두자.
2y는 사실 2 X y, 즉 2 곱하기 y이다.
몰랐어도 된다. 지금부터 알아가면 된다.
이런게 곱셈공식을 위한 기본 개념이다.
그럼 다음 그림을 보자.
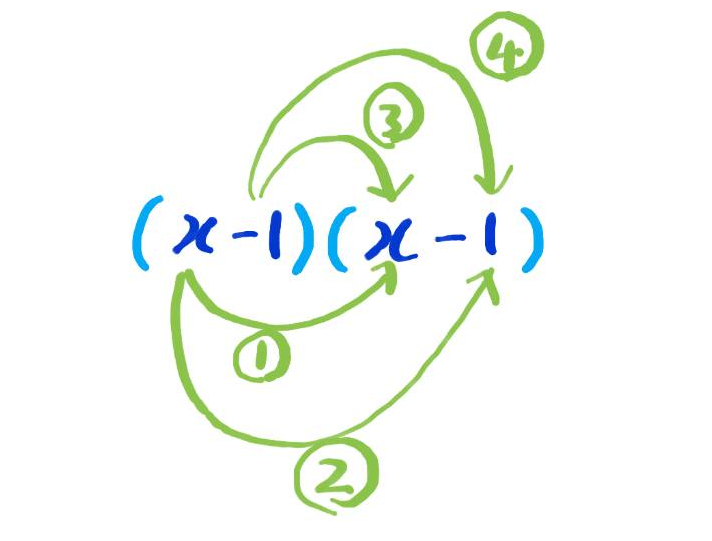
(x-1)(x-1)을 계산하는 순서를 적어놓았다.
다항식 곱하기 다항식일때는,
먼저 첫번째의 다항식의 첫째항과 두번째의 다항식의 첫째항끼리 계산을 한다. 이게 그림의 1번이다.
그다음 첫번째의 다항식의 첫째항과 두번째의 다항식의 둘째항끼리 계산을 한다. 이게 그림의 2번이다.
첫번째 다항식의 첫째항과 두번째 다항식의 항들 계산이 끝나면, 이제 첫번째 다항식의 두번째 항을 두번째 다항식의 첫번째, 두번째 항과 계산해준다. 이게 그림의 3번, 4번이다.
계산을 해보면 x곱하기x, x곱하기 -1, -1곱하기 x, -1곱하기-1 이렇게 4개의 항이 나온다.
그럼 x제곱, -x, -x, 1 이렇게 된다.
-1곱하기 -1이 왜 1이냐고?
앞에 -가 달려있는 수는 곱셈이나 나눗셈을 할때, -가 2개, 4개, 6개 이런식으로
짝수개가 있으면 서로 사라져서 +가 된다.
따라서 -1곱하기 -1은 -가 2개 있으니까 +1이 되는 것이다.
그러면 -1 나누기 -1은 뭘까? -가 2개 있으니까 1이다.
다시 돌아가서 x제곱, -x, -x, 1을 계산해주면
x제곱, -2x, 1이 된다.
이걸 연결하면
x제곱-2x+1이 된다.
두번째 2(x-1)은 어떻게 계산할까?
2곱하기 x-1이다. 2랑 x를 곱하고, 2랑 -1을 곱하면 된다.
그러면 2x랑 -2가 구해져서
2x-2가 나온다.
그러면 x제곱-2x+1+2x-2+a=x제곱
이라는 식으로 정리가 된다.
자 이제 항등식에 대해 알아보자.
항등식은 항상 (=을 기준으로 왼쪽과 오른쪽이) 같은 식이라는 뜻이다.
그런데 사진에서
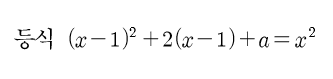
=의 왼쪽은 x제곱-2x+1+2x-2+a이었고
=의 오른쪽은 x제곱
이라는 것을 알 수 있게 되었다.
그러면 오른쪽에는 x제곱만 있으니까 왼쪽에도 x제곱만 있어야 왼쪽과 오른쪽이 같게 된다.
그럼 왼쪽에도 x제곱만 있으려면, x제곱을 제외한
-2x+1+2x-2+a가 0이 되어야 한다.
-2x랑 +2x를 계산하면 0이 되고,
+1이랑 -2를 계산하면 -1이 된다.
결국 -1+a가 0이 되어야 한다는 사실을 알 수 있다.
-1+a가 0이 되려면,
a는 1이 되어야 한다.
따라서 답은 1번이다.
글을 읽다가 모르는 내용이 생기면 언제든지 댓글로 물어봐주길 바란다.
이 글이 수포자들에게 많은 도움이 되면 좋겠다.








